Eren BillurPredicting Springback with Simulation
September 2, 2021Comments
Sounds quite easy, doesn’t it? After all, there are papers from the 1980s on predicting springback using finite-element analysis (FEA), and many commercially available software packages offer die designers easy access to FEA capabilities. Yet with all of these advancements, we still hear of shops machining die surfaces two or more times. What goes wrong?
Springback—Simple Mathematics
To understand the challenges with springback prediction, let us understand the simplest math behind it. Consider the tensile test—pulling a test specimen causes it to elongate. If the test keeps the specimen below its yield point, when removing the load the specimen’s total length should equal its original length (i.e., before the tensile test).
However, if the tensile-test load exceeds the specimen’s yield strength, its final length depends on:
1) Stress condition before load removal (σr)
2) Unloading behavior of the material (Eu).
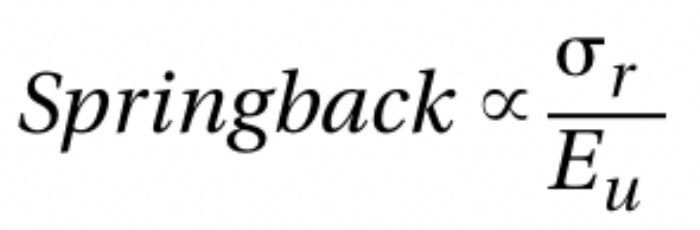
Calculating Stress
Correctly calculating the stress before removing the load requires use of a hardening curve and yield locus (see Cutting Edge, June 2021 issue of MetalForming). If the material is simply stretched (as with a tensile test), the hardening curve would be sufficient. However, if forming occurs along two axes, we also require the yield locus.
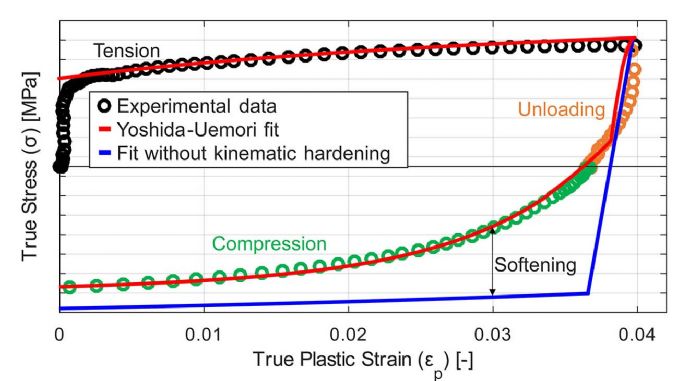
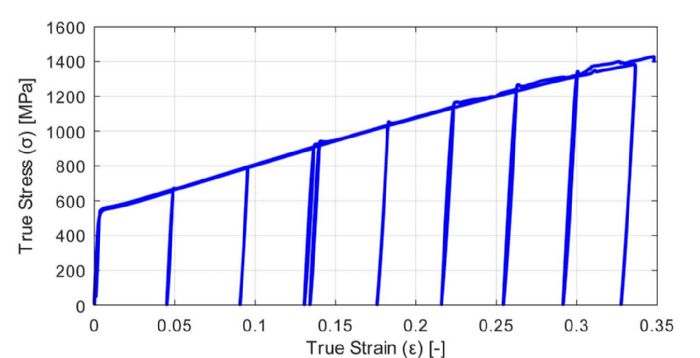
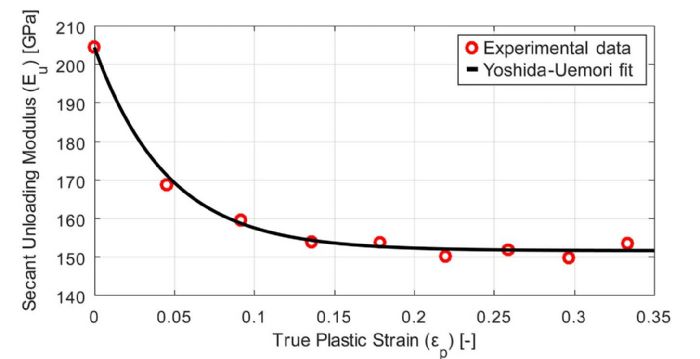
Stretching a Gen3 advanced high-strength steel (AHSS) to about 4 percent of true plastic strain and then compressing it back to 3 percent results in an approximate 40-percent reduction in the flow stress (Fig. 1). Compressing the same steel back to its original shape, the experimental flow stress is approximately 15 percent less than the prediction without kinematic hardening (Fig. 1).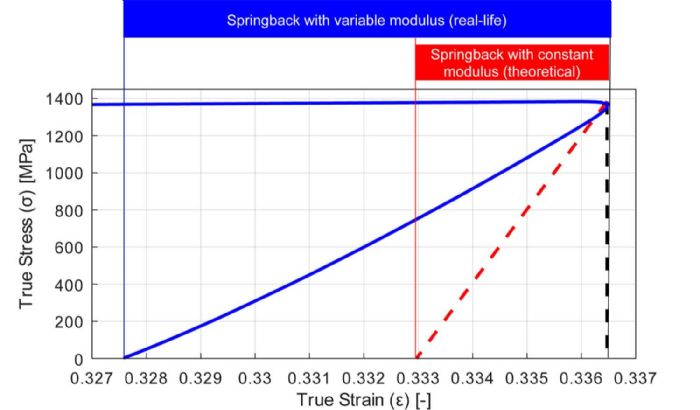 
It is clear and convincing that the unloading modulus significantly affects the ability to predict springback. Still not convinced? See Fig. 4. 
Webinar