Delta r (Δr), the planar anisotropy parameter, indicates the ability of a material to demonstrate a non-earing behavior:
Δr = (r0 + r90 - 2r45)/2
 A value of 0 is ideal for can making or for deep drawing of cylinders, as this indicates equal sheet metal flow in all directions, eliminating the need to trim ears prior to subsequent processing.
A value of 0 is ideal for can making or for deep drawing of cylinders, as this indicates equal sheet metal flow in all directions, eliminating the need to trim ears prior to subsequent processing.
High-strength steels with tensile strength greater than 450 MPa and hot-rolled steels have rm values close to 1. Therefore, conventional high-strength, low-alloy (HSLA) and advanced high-strength steels (AHSS) at similar yield strengths perform equally in forming modes influenced by the rm value. However, r-value for higher-strength grades of AHSS (800 MPa or higher) can be lower than 1, and any performance influenced by r-value would be less than that for an HSLA steel of similar strength. For example, AHSS grades may struggle to form part geometries requiring a deep draw, including corners where the steel experiences circumferential compression on the binder. This is one reason why higher-strength AHSS grades should have open-ended part-design developments.
Of note: The rm value of many aluminum alloys also is close to or less than 1.
Impact on Formability
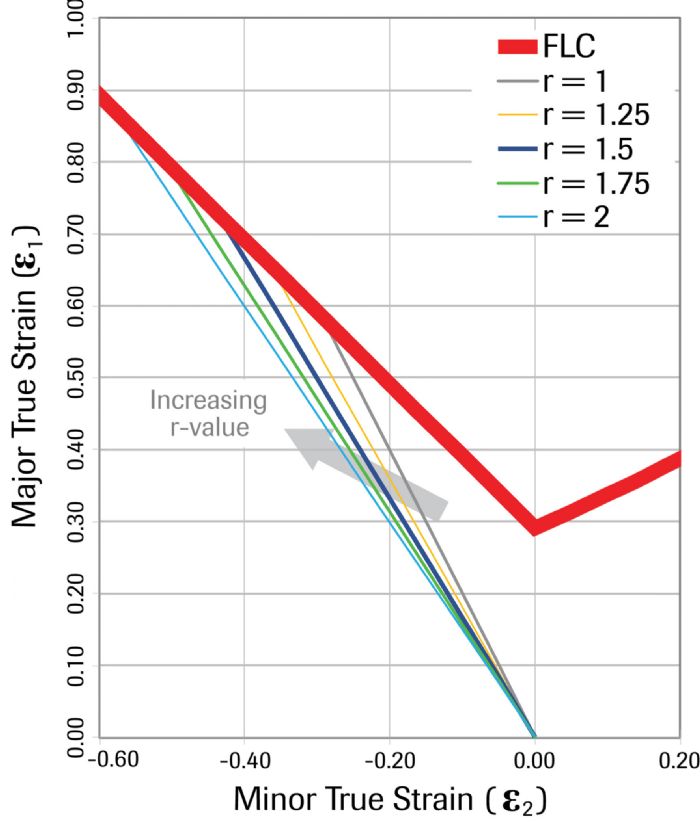
Unlike n-value when testing steels, changes in r-value do not directly affect the forming-limit curve itself. The key impact is in the uniaxial tension strain path, where higher r-value moves the slope of the strain path farther away from plane strain on the vertical axis. This means that parts now can tolerate greater major strain before necking, translating to deeper and more complex draws.
A line in true strain space characterizes the uniaxial tension strain path:
slope = – (1+r)/r
Fig. 1 shows how r-value and the associated strain-path slope impacts the achievable major strain. When forming a material with r = 1 and FLC0 = 0.29, the forming strains in the uniaxial tensile strain path reach a true major strain of 0.58 (equating to an engineering strain of 78 percent) before necking. Deforming a material with r = 2 may reach a true major strain of 0.90 (an engineering strain of 145 percent) in this strain path before necking occurs.
R-Value Influence on Cup Drawing
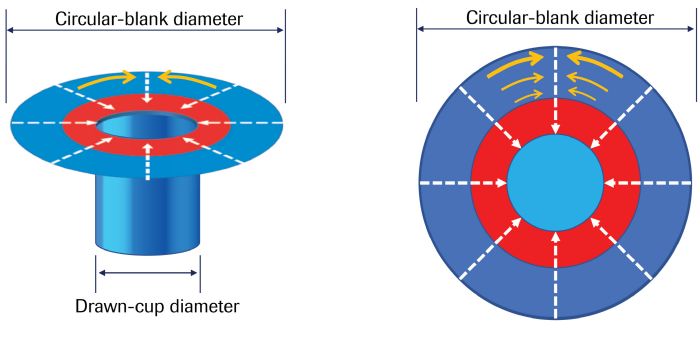
Cup drawing occurs when a cylindrical punch contacts and then pushes a circular blank into a die. Material in the blank flows over the die radius into the cup wall. The sheet metal movement from the flat blank to the vertical sidewalls (Fig. 2) is the only movement; no sheet metal flows within the flat bottom region. The flange of the circular blank undergoes radial tension and circumferential compression as the flange moves in a radial direction toward the circular die radius in response to the pull generated by a flat-bottom punch. Blankholder pressure should be set to prevent buckles in the blank, but no higher as that would restrict material flow.
Limiting draw ratio (LDR) represents the ratio of largest blank diameter (dBmax) to punch diameter (dP) that can successfully be drawn into a cup:
LDR = dBmax/dP
Factors that increase LDR include higher r-value, reduced friction coefficient (through use of a better lubricant) and a larger die-corner radius with an associated increase in the radius/thickness ratio. The biggest impact in LDR occurs with r-value; grades with high r-value deform more in the plane of the sheet and less through the thickness, which allows more deformation before thinning and tearing.
The higher r-value of mild steel results in a greater LDR compared with dual-phase steels. Transformation induced plasticity (TRIP) and 3rd Gen steels have improved LDR, which benefits deep drawability. Both steel types rely on the TRIP effect, where austenite in the microstructure transforms to martensite as a flat blank deforms into the targeted part shape. The magnitude of this transformation from plane strain deformation in the cup wall is greater than transformation from shrink flanging in the flange area, making the wall area stronger than the flange area, thereby increasing the measured LDR.
Remember that the four corners of a rectangular pan each behave as a quarter of a cup draw, so similar troubleshooting strategies and constraints apply. MF
Industry-Related Terms: Alloys,
Austenite,
Blank,
Die,
Draw,
Drawing,
Flange,
Form,
Forming,
Martensite,
Tensile Strength,
ThicknessView Glossary of Metalforming Terms
See also: Engineering Quality Solutions, Inc., 4M Partners, LLC
Technologies: Materials
 Strains of 15 to 20 percent commonly are used for determining the r-value of low-carbon sheet steel, while testing of aluminum sheets typically employs strains of 10 to 15 percent. Like n-value, the ratio will change depending on the chosen reference strain value. An r-value of 1 means that the sheet has similar response to deformation in the width and thickness directions.
Strains of 15 to 20 percent commonly are used for determining the r-value of low-carbon sheet steel, while testing of aluminum sheets typically employs strains of 10 to 15 percent. Like n-value, the ratio will change depending on the chosen reference strain value. An r-value of 1 means that the sheet has similar response to deformation in the width and thickness directions.






 A value of 0 is ideal for can making or for deep drawing of cylinders, as this indicates equal sheet metal flow in all directions, eliminating the need to trim ears prior to subsequent processing.
A value of 0 is ideal for can making or for deep drawing of cylinders, as this indicates equal sheet metal flow in all directions, eliminating the need to trim ears prior to subsequent processing.