Metal Properties: Strain-Hardening Exponent (n-Value)
January 20, 2023Comments
Plastic deformation strengthens all metal alloys. Rolling in sheet production, straightening during coil processing and stamping sheet metal into engineered part shapes all are forms of plastic deformation.
The interchangeable terms strain hardening and work hardening describe the strengthening that results from plastic deformation; the magnitude of this strengthening varies based on the alloy type and the deformation severity. Despite the terms used, this is a strengthening mechanism, not a hardening one.
Strain hardening begins once deformation exceeds the material’s yield strength and continues until the tensile-test dogbone sample or the engineered stamping either fractures or, instead, reaches the targeted strain level or part shape.
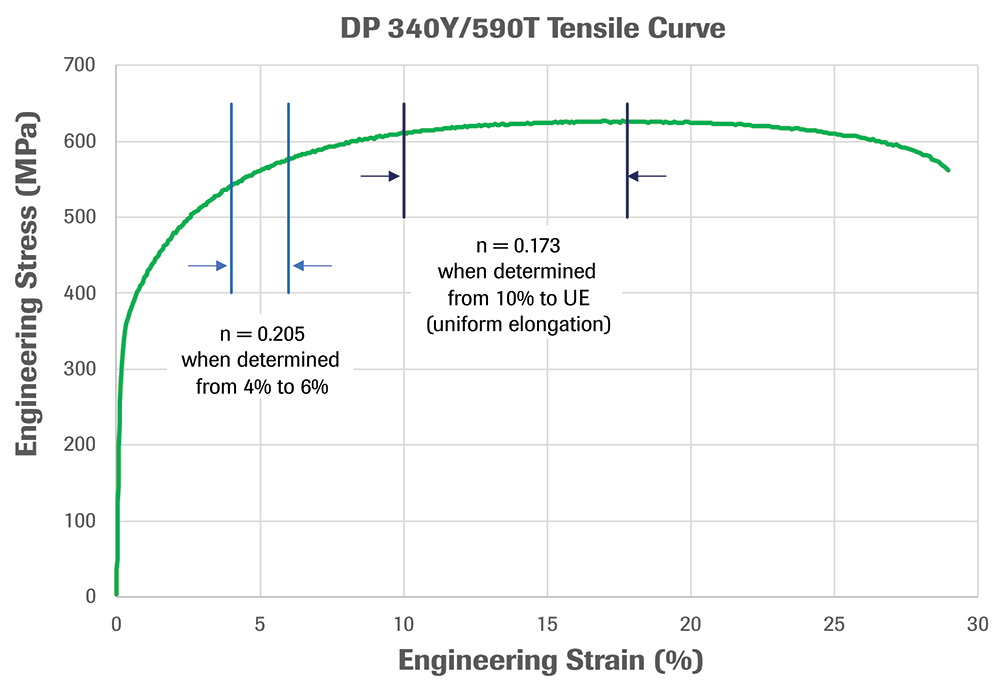The general shape of a stress-strain curve produced during tensile testing illustrates the influence of strain hardening, with the material strengthening on the vertical axis and increasing strain on the horizontal axis. Strengthening appears to stop at the tensile strength, but this perceived peak only is an artifact of the effects of the rapidly decreasing cross-sectional area of the tensile dogbone sample overpowering the increase in strain hardening.
In 1945, U.S. Army researcher John Holloman discovered a power-law relationship between stress and strain for steels (and some other metal alloys) in the region of uniform plastic deformation, which extends from the yield strength to the tensile strength:
σ = Kɛn (eq. 1)
σ, true stress; K, strength coefficient; ɛ, true strain; n, strain-hardening exponent.
Remember that true stress and true strain are based on the ever-changing dimensions as the sample or stamping deforms, as opposed to engineering stress and engineering strain where changes relate to the initial tensile-bar dimensions.
