Determining Maximum Allowable Stretch
December 1, 2009Comments
What is the maximum allowable stretch (strain) a sheetmetal blank can withstand before failure? Pose that question to people working in the metalforming industry and a variety of answers are received. Uniform elongation, total elongation and some relationship to tensile strength measured from a tensile test are the most common answers. Unfortunately, stampings almost never are shaped like a tensile test specimen. Of course, others will attempt to relate maximum allowable stretch and other behaviors to the hardness of the material. However, the size of the crater created by a punch driven into the surface by a defined load is even less related to termination of useful stretchability.
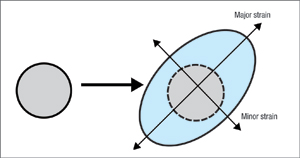 |
| Fig. 1—Strain (deformation) in the plane of the sheet is measured as a circle grid on the blank as it is deformed into an ellipse. |
First, one must be able to measure the amount of strain experienced by each element of the stamping. This is commonly done by defining the amount of strain in two specific perpendicular directions in the plane of the sheet. The easiest to determine these two directions begins with etching a pattern of circle grids into the surface of the blank. After deformation, each circle has transformed into an ellipse (Fig. 1). The long axis of the ellipse, called major strain, defines the direction and magnitude of the maximum positive strain for that circle. The direction of the major strain depends on the deformation patterns within the stamping and not on the properties or rolling direction of the blank. The axis perpendicular to the major strain, called minor strain, als defines the least strain for that circle.
A large multitude of major and minor strain combinations are possible within any given stamping. Some examples are shown in Fig. 2. The thickness strain at any ellipse can be computed from the major and minor strains using the constancy of volume rule.
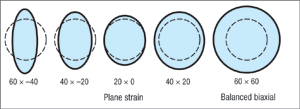 |
| Fig. 2—Examples of some combinations of major and minor strains are shown with the minor strain range limited to -40 to +60 percent. |
Worldwide studies have shown a given blank with constant tensile test properties will not have a single stretchability limit, but will have numerous stretchability limits depending on the variation in the minor strain values. Translating this multiplicity of stretching limits into a useful press shop tool is the forming limit curve (FLC). A standard-shape FLC for low-carbon steel is shown in Fig. 3. The major (largest positive) strain value is plotted vertically and the minor (smallest) strain value plotted horizontally. The points on the FLC represent possible combinations of stretching limits that could be found in a single stamping.
The FLC actually defines the onset of a local neck discussed in last month’s column. The curve shows that the maximum allowable or major strain is controlled by the value of the minor strain. In turn, the minor strain is controlled by the die design. Cylindrical cup drawing and the corner formation of a rectangular box are located at the far left of the FLC in Fig. 3. A tensile test is found to the left of the vertical axis. Stretch bending data plot on the vertical axis. Rigid punch dome stretching is to the right of the vertical axis. A hydraulic dome or bulge is located at the far right.
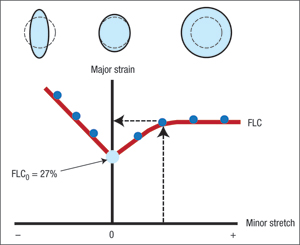 |
| Fig. 3—Forming limit curve schematic for low carbon steel shows some possible minor strain points with their corresponding allowable major strain values. |
The curve moves up or down based on the properties of the sheetmetal. The equation defining FLC0 (the lowest point on the FLC at a minor strain of zero) for low carbon steels:
FLC0 = (23.3 + 360 t) n/0.21
where t is the initial sheet thickness in decimal inches less than 0.125-in. The n-value is the work-hardening exponent discussed in the September and October columns. The equation shows that sheet thickness has a small effect on FLC0, but n-value has a direct relationship.
An interesting feature of the FLC is that the least amount of allowable stretchability occurs when the minor strain is zero. Stretching or compressing the minor strain direction increases the allowable major strain. The FLCs are experimental curves. Worldwide agreement on theories behind these curves is still lacking after several decades of press shop applications.
Up to this point, the FLC discussion has considered only low-carbon steels. These steels are one alloy (low-carbon) and one temper (dead soft or light temper passed) for different types and grades. There also are FLCs for stainless steel, aluminum, copper, brass and many other metal alloys. Unfortunately, the huge number of alloy, type, grade, thickness, and temper combinations with relatively low-volume production has not made it feasible to conduct extensive studies to obtain a critical mass of data needed to generate equations for FLC0 or even standard shape curves similar to those available for steel. Therefore, these alloys require laboratory generated experimental FLC curves for each batch of material being studied.
Many physical press shops use circle grids and FLCs to determine the severity of their stampings for die tryout, production and troubleshooting. However, the most widely accepted application of these techniques is found in the virtual press shop or computerized die tryout. Strain combinations over FLC provide a measure of forming severity and a signal for the onset of failure. Corrective actions are implemented with simple strokes of the keyboard instead of the traditional grinding and welding found in almost all physical press shops. MF
View Glossary of Metalforming Terms
Technologies: Materials









